
 Share This Page
Share This Page| Home | | Mathematics | |  |  |  Share This Page Share This Page |
Copyright © 2014, Paul Lutus — Message Page
Most recent revision: 08.14.2014
Click here for a PDF version of this article.
(double-click any word to see its definition)
This article analyzes a mathematical modeling problem in human population studies. Most mathematical treatments of population include unrealistic assumptions to make the mathematics simple enough to be understandable and useful. One such assumption is an unchanging source of sustenance for a growing population — a population's growth is constrained by a limited resource pool, but, contrary to real-world experience, the resource isn't diminished by its exploitation.
In this article I present a mathematical treatment that dynamically models the relationship between a growing population and two kinds of resource commonly seen in real-world environments: renewable and nonrenewable. Renewable resources are those that tolerate being exploited, examples solar energy and wind energy. Nonrenewable resources are those that are depleted by exploitation and eventually vanish, examples oil, minerals obtained by mining, water pumped from a water table at a rate that exhausts the table, and others.
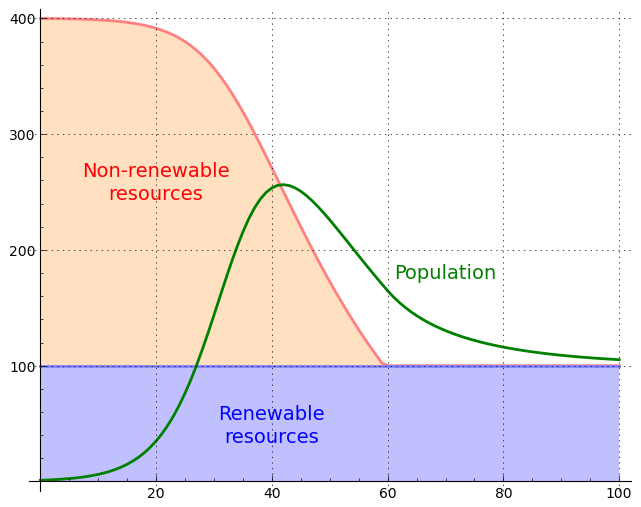
By accounting for both renewable and nonrenewable resources, this article's model predicts that the human population will reach a numerical peak and then decline as nonrenewable resources are exhausted (Figure 1). The height of the population peak above the ultimate stable population size, the velocity of the change in population and the eventual sustainable population value depend on the rate of exploitation of nonrenewable resources and the ratio of renewable to nonrenewable resources. The model accepts values for these quantities and predicts outcomes on that basis.
The idea of a population peak isn't original, but this article mathematically quantifies such a peak, using an algorithm based on the Logistic function expanded to accommodate the effect on population of nonrenewable resources.
This issue has a serious side. Unless corrective steps are taken, if nature is allowed to run her course, the post-peak decline in human numbers shown in Figure 1 may prove to be one of the worst catastrophes in human history. The alternative is a planned, gradual reduction in our numbers through voluntary population control measures, for which the Chinese one-child policy might serve as a model.
This article relies on mathematics to make its points. Readers with no interest in mathematics can skip over the mathematical sections but, by examining the graphs and text, can still follow the article's key points. (I had considered breaking this article into a nonmathematical section followed by a more technical exposition, an approach taken in some of my other articles, but the ideas presented are too dependent on mathematics for this to be practical.)
This section describes a mathematical model able to predict the behavior of an environment composed of a growing population and a mix of renewable and nonrenewable resources. It is derived from earlier mathematical work meant to model populations, in particular the Logistic function. The Logistic function is limited to describing the relationship between a growing population and a fixed resource limit, an approach having the advantage of being relatively simple, but with the drawback that it cannot accurately model many real-world biologiocal systems.
Simple Growth
For the benfit of curious readers I intend to offer a detailed explanation of this class of mathematical model, by building progressively from the simplest mathematical expressions. Again, readers with no interest in mathematics may skip over these parts of the article and still understand the points made with the graphs and text.
A growth pattern called simple growth shows a linear increase over time. A typical function would be:
(1) $p(t) = (1 + r) t$Where:
- $p(t)$ = population at time t
- $r$ = rate of increase in population
- $t$ = time in consistent units
Here's a graph of equation (1):
$r$ = 0.5Figure 2: Linear growth
Compound Growth
Equation (1) is simple and easy to understand, but biological populations grow in a different way. Because each member of a growing population can join in procreation, any increase in population is compounded over time, with an exponentially increasing source of new members. This is called compound growth or exponential growth. A typical function would be:(2) $p(t) = p_0 (1+r)^t$Where:
- $p(t)$ = population at time t.
- $p_0$ = population at time zero.
- $r$ = rate of change per unit of time.
- $t$ = time in consistent units.
Here's a graph of equation (2):
$p_0$ = 1 | $r$ = 0.5Figure 3: Exponential growth
Constrained Growth
Equation (2) models a population increase unconstrained by resource limitations, one that can expand indefinitely. But in the real world, any such population growth must eventually collide with limited resources. The classic way to model the role of environmental limitations is to apply the Logistic function:
(3) $ \displaystyle p(t) = \frac{k p_0 e^{r t}}{k+p_0 (e^{r t}-1)}$Where:
- $p(t)$ = population at time t.
- $p_0$ = population at time zero.
- $k$ = environmental carrying capacity.
- $r$ = population growth rate.
- $t$ = time in consistent units.
About equation (3) it is important to note that:
(4) $\displaystyle \lim_{t \to \infty} p(t) = k$In other words, over time the population $p(t)$ converges on the environmental carrying capacity $k$.
Here's a graph of equation (3):
$p_0$ = 1 | $k$ = 100 | $r$ = 0.1Figure 4: Constrained growth
Examine the graph of equation (3). At the left (0 <= t <= 40), the curve shows the unconstrained growth of equation (2). In the middle the growth rate becomes linear as resource limitations become important, and at the right (60 <= t <= 100), environmental constraints prevent a population greater than carrying capacity k.
Above we modeled population growth in the classic way, by setting a fixed resource limit / upper population bound. In this section we will model a system having a mixture of renewable and nonrenewable resources. This system has the following properties:
- Population increase follows the general pattern set out above — an exponential increase until resource limitations prevent further growth.
- A renewable carrying capacity $k_r$ exists as in equation (3) above, a value that does not change.
- A nonrenewable carrying capacity $k_n$ behaves in much the same way as $k_r$, except that over time the increasing population exhausts it, usually reducing it to zero.
- The presence of a nonrenewable capacity allows an unsustainable population peak that must eventually decline along with the nonrenewable resources (Figures 1 and 6).
- The long-term outcome should agree with equation (3), i.e. $ \displaystyle \lim_{t \to \infty} p(t) = k_r$.
Because of the complexity of this system, and because one of the variables ($k_n$) declines to zero and then stops changing, there's no closed-form expression to describe it — it must be modeled numerically. For maximum portability I've chosen Python to express the numerical algorithm. Here's an excerpt from a Python program able to model the described system (click here for the full listing):
kr = 100 # renewable carrying capacity kn = 300 # nonrenewable carrying capacity nr = .04 # nonrenewable rate of consumption p = 1 # initial population r = .05 # population growth rate per period for t in range(101): p *= 1 + r * (kn+kr-p)/kr # see note 2 below kn = max(kn-p * nr,0) # see note 3 belowNotes:
- If the nonrenewable capacity value is set to zero, the above numerical algorithm produces essentially the same results as the closed-form Logistic function, for given input values and using suitably small increments of time.
- This code line increases the population size by the rate of increase multiplied by a normalized capacity value from which the prior population size has been subtracted.
- This code line reduces the nonrenewable capacity value $k_n$ in proportion to population, times a nonrenewable consumption constant $n_r$. Over time this reduces the nonrenewable capacity value to zero, after which the max() function prevents it from falling below zero.
Here's a graph of the result generated by this Python program:
Renewable capacity | Nonrenewable capacity | Population$p_0$ = 1 | $k_r$ = 100 | $k_n$ = 300 | $n_r$ = 0.04 | $r$ = 0.05
Figure 6: Peak population
Interested readers are encouraged to run the provided program and change its values to see how this changes the modeled outcome. Again, if $k_n$ is set to zero and if sufficiently small time steps are used, the algorithm's results converge with that from the closed-form Logistic function, showing that it accurately reflects the outcome of the classic population function.
Now that we can use cheap computer power to model the real-world dynamics created by a mixture of renewable and nonrenewable carrying capacity, we should choose realistic values for the model. What's the true ratio of renewable ($k_r$) to nonrenewable ($k_n$) capacity? How much nonrenewable capacity consists of luxuries and how much is critical to human survival? What's the true consumption rate ($n_r$) for nonrenewable capacity? None of these questions have clear answers. The model presented here can generate useful predictions, but only with reliable values for its parameters.
Unfortunately, virtually every aspect of this issue is distorted by politics and emotion. One regularly hears claims about future human numbers without discussing sustainability, and without acknowledging that we may already be beyond a sustainable human population size. Recent population studies conclude that the present (2014) human population may be as much as three times its sustainable value, which means the example graphs in this article may accurately reflect our future.
Population and birthrate are classic examples of problems that are easy to state but very difficult to solve. History teaches us that large-scale social solutions to population problems tend to be undermined by partisan politics and racism. It's my view that individual choices, accompanied by full rights and universal education, are the only civilized solutions to this problem.
There's a technical issue that's not addressed in the above exposition, and that is the identity of the new function. If this new function is a consistent extension of the Logistic function with an added nonrenewable resource term, then by setting the initial nonrenewable value to zero it should produce the same results as the classic Logistic function. If the new function were expressible in closed form, the task of demonstrating the relationship between the two functions would be much easier, but the Logistic function is a classic closed-form solution to a differential equation, and the new function is a numerical differential equation, an algorithm, that is inexpressible in closed form.
This means a comparison between the two functions must be carried out numerically, by comparing results rather than equations. In this section I will numerically compare the results for the classic and revised functions. To acquire a meaningful comparison, I will run the algorithm with many very small increments, and show a sample of comparisons between the revised function and the classic Logistic function. The logic behind a large number of increments is that, as one approaches an infinite number of infinitesimal steps, the relationship between a summation and a definite integral converge:
(5) $ \displaystyle \displaystyle \lim_{n \to \infty} \frac{b-a}{n+1} \sum_{x = 0}^n f((b-a)\frac{x}{n}+a) = \int_a^b f(x)\, dx$For this Python test program, we get this result:t |1-a/b| --------------------- 0 0.00000099 1000000 0.00000050 2000000 0.00000006 3000000 0.00000027 4000000 0.00000037 5000000 0.00000024 6000000 0.00000008 7000000 0.00000000 8000000 0.00000001 9000000 0.00000001 10000000 0.00000001Where:
- t = Time argument.
- |1-a/b| = Absolute difference (error value) between classic Logistic function result and that for the extended Logistic function presented here.
In further tests, as the number of iterations is increased, the results show a convergence between the classic and extended forms of the Logistic equation.
- Logistic Function — a key mathematical method used to model growing populations.
- Exponential Growth — also known as compound growth.
- One-child policy — a moderately successful Chinese population control program.
- Human overpopulation | Carrying capacity — this article suggests that the present (2014) human population may be three times greater than a sustainable value.
| Home | | Mathematics | |  |  |  Share This Page Share This Page |